流体中颗粒的布朗运动是生物和物理系统中常见的集体行为。在一个关于科学进步的新报告中,李启冲和中国物理学,工程学和航空航天工程学的研究团队进行了实验和数值模拟,以显示涡旋的运动如何类似于惯性布朗粒子。在实验过程中,旋转的湍流对流涡流使颗粒首先在直接行为过渡的关键时刻弹道运动,然后在关键时间之后扩散扩散-无需经历流体动力记忆机制。这项工作意味着对流涡流具有惯性诱发的记忆,因此它们的短期运动首次在布朗运动的框架内得到了明确定义。
布朗运动
爱因斯坦(Albert Einstein)于1905年首次提出了布朗运动的理论解释,其中花粉颗粒在热浴中运动,这种现象现在已成为自然界中广泛发生的随机过程的常见例子。1908年晚些时候,保罗·兰格文(Paul Langevin)注意到了粒子的惯性,并预测它们的运动将在短时间内成为弹道运动,并在特定的时间轴后变为散射运动。但是,由于这种转变的迅速性,花了一个多世纪使研究人员能够直接观察到这种现象。然而,在液体系统中未观察到兰格文预测的“纯”布朗运动,并且该转变跨越了很宽的时间范围。由于流体动力记忆效应,发生了缓慢而平稳的过渡,最终产生了长程相关性。科学家此前曾观察到在多个系统中的水动力记忆效应,包括胶体悬浮液,悬浮在空气中的颗粒和捕获在光镊中的颗粒。在这项工作中,Chong等。首次展示了高连通性流动中的涡流如何作为惯性粒子来执行纯布朗运动,而不受流体动力效应的影响。他们使用Q准则(涡流识别方法)识别并提取了涡流。这项工作将帮助他们预测天文学和地球物理系统在特定时间段内的涡旋运动。
旋转罗利·伯纳德对流和涡的水平运动
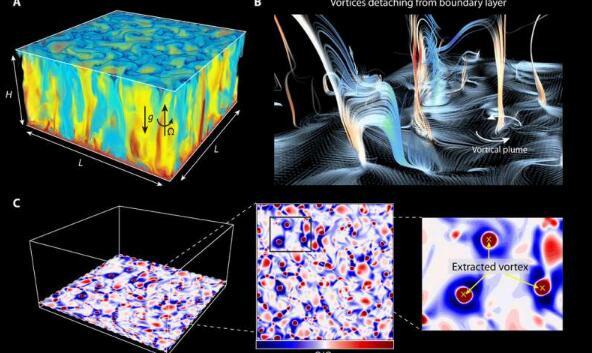
天体物理和地球物理研究中存在的一项挑战是预测特定时期内涡旋的运动。崇等。我们使用一个模型系统研究了称为Rayleigh Benard(RB)对流的对流中的涡流,该流包括固定高度的流体层,该流体层从下方加热并从上方冷却,同时围绕垂直轴以角速度旋转。当热驱动足够强时,系统中的温度差会使对流的流量不稳定。科学家使用三个无量纲参数来表征流动动力学,包括瑞利数(Ra),普朗特数(Pr)和埃克曼数(Ek)。在旋转的情况下,涡旋结构作为流体包裹螺旋上升或下降而出现。由于它们在动量和热传递中的重要性,研究人员继续对其进行研究。
崇等。首先通过一系列快照跟踪涡旋的位置变化来研究涡旋的运动。他们使用均方位移(MSD)表征了涡旋的统计行为。不同Ek和Ra的MSD值表现出相似的行为,表明旋涡运动在很短的时间内从弹道运动转变为扩散运动。这种转变类似于在热浴中的布朗运动。因此,科学家将涡旋视为布朗粒子,并通过求解朗文方程来描述其运动。获得他们的MSD。结果暗示了Ra和Ek的涡旋运动具有相似的动力学,表明涡旋表现出“纯布朗”行为。在对流系统中,涡流携带的流体包裹比周围的流体温度高和低。实验中温度变化引起的相对较小的密度差导致了明显的弹道行为。
涡流分布
尽管有类似布朗运动,但涡流的空间分布并不是随机的,并且表现出图案化的结构,这是科学家使用几种旋转速率的快照获得的。随着埃克曼数(Ek)的变化,涡旋分布发生了一些变化。首先,涡旋的数量随旋转速度的增加而增加,因此最初稀释且随机分布的涡旋变得高度集中和聚集。旋涡数密度随转速的增加也与以前的研究一致。接下来,当旋转速度变得足够高时,它们形成涡流格栅结构。当崇等。放大到一个局部区域以观察最高的旋转速度,他们观察到了这种涡流格栅结构的规则图案。涡流的红色区域形成了方格,并且在蓝色之间的局部区域显示出高应变行为。该团队将工作中观察到的正方形图案归功于不同的边界设置和控制参数。
尽管在时域中有随机运动,但涡流显示出特定的空间顺序,这导致了明显的矛盾。崇等。在慢速和快速旋转过程中观察到了涡流的轨迹。但是,旋涡的传播距离不足以“看到”或与其他旋涡相互作用。他们将漩涡的空间顺序归因于两个动力学过程之间的竞争,这两个过程分别以漩涡的弛豫时间尺度和布朗时间尺度为特征。
这样,Kai Leong Chong及其同事展示了旋转热对流中涡旋的运动如何类似于执行布朗运动的惯性粒子。运动经历了从弹道到扩散区的急剧转变,而没有经历中间的流体动力存储区。Paul Brownevin首先预测了纯布朗运动的观测,尽管在实践中液体系统中的惯性粒子以前并未观测到。这项工作强调了现有的经典理论工作,这些工作表明被动痕迹如何表现出从弹道到扩散行为的转变,类似于本研究的实验观察。观察到的纯布朗运动也表明了水动力记忆效应的微不足道。崇等。认为由于科里奥利力与自然现象中涡旋形成的相关性,包括大气中的热带气旋,海洋涡旋和木星中长寿的巨大红色斑点,科里奥利力在研究过程中具有相关性。这些发现将影响天体物理学,地球物理学和气象学的许多情况。
 教育新闻网
教育新闻网














