中学知识：角平分线性质定理及证明方法

三角形其中一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线。接下来分享角平分线性质定理及证明方法。

1.角平分线可以得到两个相等的角。

2.角平分线上的点到角两边的距离相等。

3.三角形的三条角平分线交于一点，称作三角形内心。三角形的内心到三角形三边的距离相等。

4.三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。

1.角平分线线上的点到角两边的距离相等。

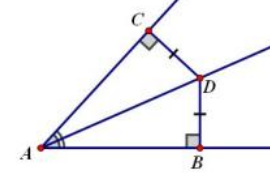
若射线AD是∠CAB的角平分线，求证：CD=BD

∵∠DCA=∠DBA

∠CAD=∠BAD

AD=AD

∴△ACD≌△ABD

∴CD=BD

2.三角形内角平分线分对边所成的两条线段，和两条邻边成比例

在三角形ABC中，当AD是顶角A的角平分线交底边于D时，BD/CD=AB/AC。

证明：

如图，AD为△ABC的角平分线，过点D向边AB,AC分别引垂线DE,DF.则DE=DF。

S△ABD：S△ACD=BD/CD

又因为S△ABD：S△ACD=[(1/2)AB×DE]：[(1/2)AC×DF]=AB：AC

所以BD/CD=AB/AC。