中学知识：重心的性质及证明

重心到顶点的距离与重心到对边中点的距离之比为2：1。重心和三角形3个顶点组成的3个三角形面积相等。重心到三角形3个顶点距离平方的和最小。(等边三角形）重心是三角形内到三边距离之积最大的点。

1、重心到顶点的距离与重心到对边中点的距离之比为2：1。

证明：已知：△ABC，E、F是AB，AC的中点。EC、FB交于G。

求证：EG=1/2CG

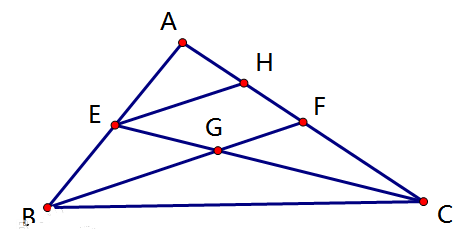
证明：过E作EH∥BF交AC于H。

∵AE=BE，EH//BF

∴AH=HF=1/2AF(平行线分线段成比例定理)

又∵ AF=CF

∴HF=1/2CF

∴HF:CF=1/2

∵EH∥BF

∴EG:CG=HF:CF=1/2

∴EG=1/2CG

2、重心和三角形3个顶点组成的3个三角形面积相等。

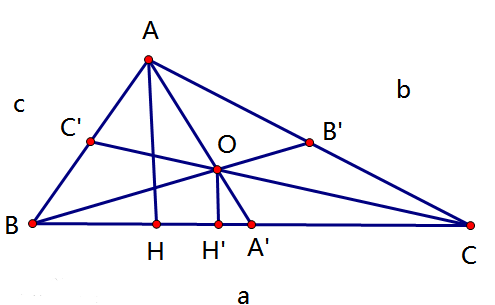
证明方法：

在△ABC内，三边为a，b，c，点O是该三角形的重心，AOA'、BOB'、COC'分别为a、b、c边上的中线。根据重心性质知：

OA'=1/3AA'

OB'=1/3BB'

OC'=1/3CC'

过O，A分别作a边上高OH'，AH

可知OH'=1/3AH

则，S△BOC=1/2×OH'a=1/2×1/3AHa=1/3S△ABC

同理可证S△AOC=1/3S△ABC

S△AOB=1/3S△ABC

所以，S△BOC=S△AOC=S△AOB

3、三角形内到三边距离之积最大的点。

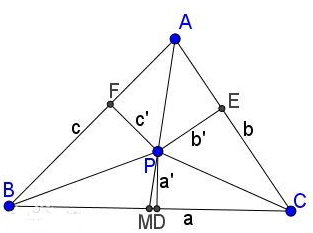
证明：点P是△ABC内的一点，连接PA，PB，PC，作点P到BC、AC、AB的垂线段，垂足分别为D、E、F，延长AP交BC于M。记△ABC的面积为S，BC为a，AC为b，AB为c，PD为a'，PE为b'，PF为c'。

∵aa'/2+bb'/2+cc'/2=S△BCP+S△ACP+S△ABP=S

∴aa'+bb'+cc'=2S

由均值不等式知，[(aa'+bb'+cc')/3]^3≥aa'bb'cc'=(abc)*(a'b'c')，当且仅当aa'=bb'=cc'时等号成立。

∴a'b'c'≤[(aa'+bb'+cc')/3]^3/(abc)=(S/3)^3/(abc)=8S^3/(27abc)，当且仅当aa'=bb'=cc'时等号成立。

∴a'b'c'惟独当aa'=bb'=cc'时才会取得最大值。

此时，S△ABP=cc'/2=bb'/2=S△ACP，由燕尾定理知，BM/CM=S△ABP/S△ACP=1。

∴此时BM=CM，M是BC的中点，AM是△ABC的中线，P在△ABC中BC边的中线上。

同理可证此时P在△ABC中AB、AC边的中线上。

∴当a'b'c'最大时，P是△ABC的重心，即重心是三角形内到三边距离之积最大的点。