中学知识：勾股定理证明最简单的方法

勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。那么勾股定理证明最简单的方法有哪些呢？下面就和小编一起了解一下吧，供大家参考。

证法一：

这是最简单精妙的证明方法之一，几乎不用文字解释，可以说是无字证明。如图所示，左边是4个相同的直角三角形与中间的小正方形拼成的一个大正方形。

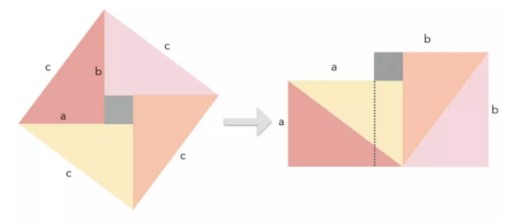
图形变换后面积没有变化，左边大正方形的边长是直角三角形的斜边c，面积是c2；右边图形可分割为两个正方形，它们的边长分别为直角三角形的两条直角边a和b，面积就是a2＋b2，于是a2＋b2＝c2。

图中左边的“弦图”最早浮现在公元222年的中国数学家赵爽所著《勾股方圆图注》，赵爽是我国数学史上证明勾股定理的第一人。2002年8月，在北京召开的国际数学家大会，标志着中国数学进入崭新的时代，大会会徽就是这个“弦图”，寓意中国古代数学取得的重要成果。

证法二：

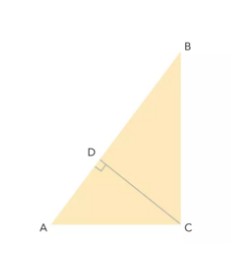
证法三：

这一证法涉及到圆内相交弦定理：m·n＝p·q（如左图），再看AB和CD垂直的情况，相交弦定理仍然成立（如右图），因此(c－a)(c＋a)＝b2。即得c2－a2＝b2于是，a2＋b2＝c2。

勾股定理，公式表达为：a²+b²=c²，其中a、b分别为直角边，c直角三角形的斜边。譬如a=3，b=4，那么得c=5。这个三角形的面积S=ab/2=3×4/2=6。

勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。